L

1. Mesure du diamètre de la Lune

La première mesure de la taille de la Lune et de la distance Terre-Lune a été réalisée dès l'antiquité au moyen de l'observation des éclipses.

    1.1. Les éclipses de Lune

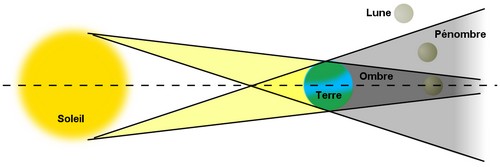
Une éclipse de Lune se produit à chaque fois que la Lune se trouve dans l'ombre de la Terre. Ceci se produit uniquement lorsque la Lune est pleine, et quand le Soleil, la Terre et la Lune sont parfaitement alignés ou proches de l’être.

Si le plan de l´orbite de la Lune était le même que le plan de l´orbite de la Terre (écliptique), il y aurait une éclipse de Lune à chaque pleine Lune, or le plan de l´orbite de la Lune est incliné d´environ 5° 17' sur le plan de l´orbite terrestre à la pleine Lune. L´intersection de ces deux plans est une droite appelée ligne des noeuds et les intersections de cette droite avec l´écliptique sont appelées noeuds de l´orbite lunaire. Pour qu´il y ait une éclipse, il faut donc que la Lune soit près de la ligne des noeuds au moment de la pleine Lune.

En fonction de la position relative de la Lune par rapport à la ligne des noeuds, on peut observer différentes éclipses : éclipses dans la pénombre, éclipses totales ou partielles.

Dans le cas d'une éclipse totale, les différentes phases sont les suivantes :

P1 : entrée dans la pénombre , P2 : sortie de la pénombre, O1 : entrée dans l'ombre , O2 : sortie de l'ombre

T1 : début de la totalité , T2 : fin de la totalité, M : maximum de l'éclipse

Cliquer ici pour observer les différentes phases de l'éclipse du 3 mars 2007.

    1.1. Les mesures d'Hipparque

Cliquer sur l'image d'Hipparque pour découvrir les mesures qu'il a effectuées.

2. Mesure de la circonférence de la Terre par la méthode d'Eratosthène (-276,-194)

    2.1. Sphéricité de la Terre

L'idée que la Terre est une sphère est déjà admise à l'époque d'Eratosthène.

Il ne fut pas le premier à émettre cette hypothèse.

La sphéricité de la Terre est généralement attribuée à l'école pythagoricienne dès le VI° siècle avant J.C.

Une des preuves de la sphéricité de la Terre fut apportée lors de l'observation d'éclipses de Lune.

Lorsque la Lune entre dans l'ombre de la Terre, on peut observer la projection de cette ombre sur la Lune.

Elle décrit un arc de cercle.

    2.2. Méthode d'Eratosthène

Eratosthène déduisit la circonférence de la Terre (ou méridien terrestre) d'une manière purement géométrique.

Il observa l'ombre de deux objets situés en deux lieux, Syène (aujourd'hui Assouan) et Alexandrie, le 21 juin (solstice d'été) au midi solaire local.

C'est à ce moment précis de l'année que dans l'hémisphère nord le Soleil détient la plus haute position au-dessus de l'horizon.

Eratosthène remarqua qu'il n'y avait aucune ombre à Syène (ville située à peu près sur le tropique du Cancer). Ainsi, à ce moment précis, le Soleil était vertical et sa lumière éclairait directement le fond du puits.

Eratosthène remarqua cependant que le même jour à la même heure, un obélisque situé à Alexandrie formait une ombre ; le Soleil n'était donc plus à la verticale et l'obélisque avait une ombre décentrée.

Par des calculs de trigonométrie, il déduisit que l'angle entre les rayons solaires et la verticale était de 7,2 degrés.
 

Eratosthène évalua ensuite la distance entre Syène et Alexandrie en faisant appel à un bématiste qui se basa sur le temps en journées de marche de chameau entre les deux villes : la distance obtenue était de 5000 stades, soit environ 800 km, mesure très proche de la réalité, un stade (longueur utilisée dans les stades d'Olympie ou de Delphes) valant environ 157,5 m.

Par la théorie géométrique des angles alternes-internes, Eratosthène proposa une figure d'une éblouissante simplicité : elle était composée d'un simple cercle ayant un angle au centre de 7,2 degrés qui intercepte un arc (reliant Syène à Alexandrie) de 800 km.

Cliquer sur l'icône ci-dessous pour découvrir le calcul d'Eratosthène commenté.

Le résultat d'Eratosthène est extraordinairement précis pour l'époque. Les mesures actuelles donnent 40075 km à l'équateur et 40008 km en passant par les pôles.

Cliquer ici pour revoir (en anglais !) toute la démarche d'Eratosthène.